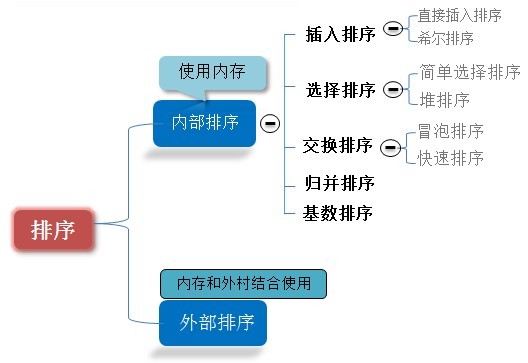
1：明确有多少个基础排序算法

</br>

通常我们使用的是内部排序：
a:插入排序—直接插入排序 希尔排序
b:选择排序—简单选择排序 堆排序
c:交换排序—冒泡排序 快速排序
d:归并排序
e:基数排序

那么什么是外部排序呢？为什么要用到外部排序呢？通常数据量太大太大，内存塞不进全部数据的时候采取外部排序。 把排序好的数据和未排序好的数据放到硬盘中储存。
外部排序指的是大文件的排序，即待排序的记录存储在外存储器上，待排序的文件无法一次装入内存，需要在内存和外部存储器之间进行多次数据交换，以达到排序整个文件的目的。

2:下面是我们讲解的排序

a:直接插入排序

//插入排序
func insertSort(numbers []int) {
    i, j := 0, 0
    n := len(numbers)
    for i = 1; i < n; i++ {
        temp := numbers[i]                //选取基点
        j = i - 1                         //i的上一个点
        for j >= 0 && temp < numbers[j] { //5 12 17 3 10 7 14 9 11 15 0 19 2 1 13 4 16 6 18 8
            //temp = 12 ,i=1;j=0; number[j]=5;temp=12; 就是把大的数据移到后面去
            numbers[j+1] = numbers[j] //循环 把 j后面的数字 移到前面去，只要
            j--
        }
        numbers[j+1] = temp
    }
    fmt.Println(numbers)

}

插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

步骤：

1:从第一个元素开始，该元素可以认为已经被排序
2:取出下一个元素，在已经排序的元素序列中从后向前扫描
3:如果该元素（已排序）大于新元素，将该元素移到下一位置
3:重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5:将新元素插入到该位置中
6:重复步骤2

b:希尔排序

//希尔排序
func shellSort(numbers []int) {
    n := len(numbers)
    var i, j, gap, temp int
    gap = n / 2
    for gap > 0 {
        for i = gap; i < n; i++ {
            temp = numbers[i]
            j = i - gap
            for j >= 0 && temp < numbers[j] {
                numbers[j+gap] = numbers[j]
                j = j - gap
            }
            numbers[j+gap] = temp
        }
        gap = gap / 2
    }
    fmt.Println(numbers)
}

介绍：

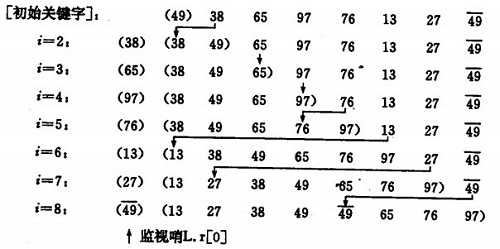
希尔排序，也称递减增量排序算法，是插入排序的一种高速而稳定的改进版本。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

1、插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率

2、但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位

排序效果：

c:简单选择排序

暂时无代码

介绍：

选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。 1:首先在未排序序列中找到最小元素，
2:存放到排序序列的起始位置，
3:然后，再从剩余未排序元素中继续寻找最小元素，
4:然后放到排序序列末尾。以此类推，直到所有元素均排序完毕。

排序效果：

d:冒泡排序

//冒泡排序 交换排序
func defaultsoft(numbers []int) {
    fmt.Println(numbers)
    temp := numbers[0]
    len_number := len(numbers)
    for i := 0; i < len_number-1; i++ { //注意数据越界
        for j := len_number - 1; j > i; j-- {
            if numbers[j] > numbers[i] {
                temp = numbers[j]
                numbers[j] = numbers[i]
                numbers[i] = temp
            }
        }
    }
    fmt.Println(numbers)
}

介绍：

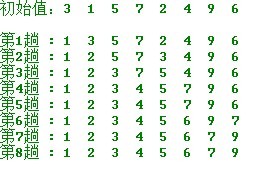
冒泡排序（Bubble Sort，台湾译为：泡沫排序或气泡排序）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

步骤：

1：比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2：对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3：针对所有的元素重复以上的步骤，除了最后一个。
4：持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

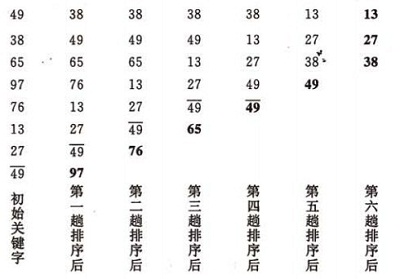
排序效果：

e:快速排序

//快速排序 在某一段范围内排序 [s,t]
func quickSort(numbers [] int,s int ,t int){
    i:=s
    j:=t
    fmt.Println(numbers)
    var temp int
    if s < t{//区间内至少存在俩个元素的情况
        temp = numbers[s];//用区间的第一个记录作为基准
        fmt.Println("基准",temp)
        for i!=j{//从俩端交替向中间扫描，直到i=j为止
            for j > i && numbers[j] >temp{//从右向左扫描，找到第一个小于temp的number[j]
                j--
            }
            numbers[i]=numbers[j]//找到这样的number[j],number[j]/number[i]交换
            for i <j && numbers[i] <temp{//从左向右扫描，找到第一个大于temp的number[i]
                i++
            }
            numbers[j]=numbers[i]//找到这样的number[i],number[i]/number[j]交换
        }
        numbers[i]=temp
        quickSort(numbers,s,i-1)//对左区间递归排序
        quickSort(numbers,i+1,t)//对右区间递归排序
    }
}

介绍：

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

步骤：

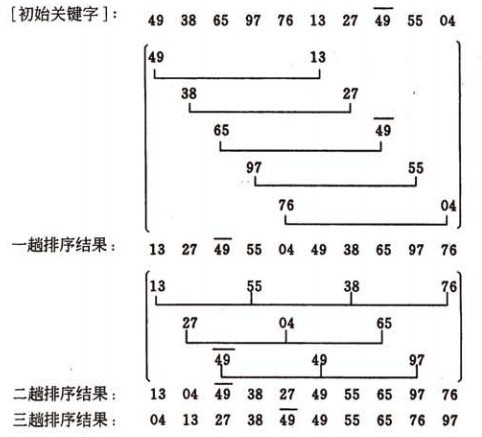
1:从数列中挑出一个元素，称为 “基准”（pivot）
2:重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3:递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

(a):一趟排序的过程：

(b):排序的全过程 ：

排序效果：

f:堆排序

暂无代码

介绍：

堆积排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

最大堆和最小堆问题

排序效果：

g:归并排序

介绍：

归并排序（Merge sort，台湾译作：合并排序）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用

步骤：

1：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2：设定两个指针，最初位置分别为两个已经排序序列的起始位置
3：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4：重复步骤3直到某一指针达到序列尾
5：将另一序列剩下的所有元素直接复制到合并序列尾

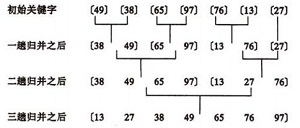</br> 排序效果：

总结

各种排序的稳定性，时间复杂度和空间复杂度总结：

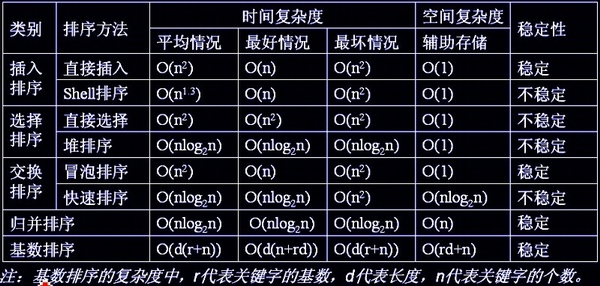
比较时间复杂度函数的情况：

时间复杂度来说：

(1)平方阶(O(n2))排序
　　各类简单排序:直接插入、直接选择和冒泡排序；
(2)线性对数阶(O(nlog2n))排序
　　快速排序、堆排序和归并排序；
(3)O(n1+§))排序,§是介于0和1之间的常数。
　　希尔排序
(4)线性阶(O(n))排序
　　基数排序，此外还有桶、箱排序。

说明：

当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O（n）；

而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O（n^2）；

原表是否有序，对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

选择排序算法准则：

每种排序算法都各有优缺点。因此，在实用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。

选择排序算法的依据

影响排序的因素有很多，平均时间复杂度低的算法并不一定就是最优的。相反，有时平均时间复杂度高的算法可能更适合某些特殊情况。同时，选择算法时还得考虑它的可读性，以利于软件的维护。一般而言，需要考虑的因素有以下四点：

1．待排序的记录数目n的大小；
2．记录本身数据量的大小，也就是记录中除关键字外的其他信息量的大小；
3．关键字的结构及其分布情况；
4．对排序稳定性的要求。

设待排序元素的个数为n.

1）当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
堆排序 ：  如果内存空间允许且要求稳定性的，   
归并排序：它有一定数量的数据移动，所以我们可能过与插入排序组合，先获得一定长度的序列，然后再合并，在效率上将有所提高。  

2） 当n较大，内存空间允许，且要求稳定性 =》归并排序

3）当n较小，可采用直接插入或直接选择排序。

直接插入排序：当元素分布有序，直接插入排序将大大减少比较次数和移动记录的次数。   
直接选择排序 ：元素分布有序，如果不要求稳定性，选择直接选择排序   

5）一般不使用或不直接使用传统的冒泡排序。

6）基数排序
它是一种稳定的排序算法，但有一定的局限性：

1、关键字可分解。   
2、记录的关键字位数较少，如果密集更好   
3、如果是数字时，最好是无符号的，否则将增加相应的映射复杂度，可先将其正负分开排序。    

7)end